Journal Publications
- Ivica Nakić, Zoran Tomljanović, Ninoslav Truhar
- Optimal Direct Velocity Feedback
- Applied Mathematics and Computation 225 (2013) ; 590-600
Preliminary version appeared as Preprint 3/2013, Department of Mathematics, J. J. Strossmayer University of Osijek. (*.PDF) -
ABSTRACT: We present a novel approach to the problem of Direct Velocity Feedback (DVF) optimization of vibrational structures, which treats simultaneously small as well as large gains. For that purpose, we use two different approaches. The first one is based on the gains optimization using the Lyapunov equation. In the scope of this approach we present a new formula for the optimal gain and we present a relative error for modal approximation. In addition, we present a new formula for the solution of the corresponding Lyapunov equation for the case with multiple undamped eigenfrequencies, which is a generalization of existing formulae. The second approach studies the behavior of the eigenvalues of the corresponding quadratic eigenvalue problem. Since this approach leads to the parametric eigenvalue problem we consider small and large gains separately. For the small gains, which are connected to a modal damping approximation, we present a standard approach based on Gerschgorin discs. For the large gains we present a new approach which allows us to approximate all eigenvalues very accurately and efficiently.
- Ivana Kuzmanović, Zoran Tomljanović, Ninoslav Truhar
- Optimization of material with modal damping
- Applied Mathematics and Computation
218 (2012); 7326-7338
Preliminary version appeared as Preprint 9/2010, Department of Mathematics, J. J. Strossmayer University of Osijek. (*.PDF) -
ABSTRACT: This paper considers optimal parameters for modal damping $D=Mf_1(M^{-1}K;\alpha_1,\dots,\alpha_k)+Kf_2(K^{-1}M;\alpha_1,\dots,\alpha_k)$ in mechanical systems described by the equation $M\ddot{x}+D\dot{x}+Kx=0 $, where matrices $M$ and $K$ are mass and stiffness matrices, respectively. Different models of proportional and generalized proportional damping are considered and optimal parameters with respect to different optimization criteria related to the solution of the corresponding Lyapunov equation are given. Also, some specific example problems are compared with respect to the optimal and estimated parameters.
- Peter Benner, Zoran Tomljanović, Ninoslav Truhar
- Optimal Damping of Selected Eigenfrequencies Using Dimension Reduction
- Numerical Linear Algebra with Applications, 20 (2013) , 1; 1-17 , Published online in Wiley Online Library. DOI: 10.1002/nla.833
Preliminary version appeared as Preprint 1/2011, Department of Mathematics, J. J. Strossmayer University of Osijek. (*.PDF) -
ABSTRACT: We consider a mathematical model of a linear vibrational system described by the second-order differential equation $M \ddot{x} + D \dot{x} + Kx = 0$, where $M$ and $K$ are positive definite matrices, representing mass and stiffness, respectively. The damping matrix $D$ is positive semidefinite. We are interested in finding an optimal damping matrix which will damp a certain (critical) part of the undamped eigenfrequencies. For this we use an optimization criterion based on minimization of the average total energy of the system. This is equivalent to the minimization of the trace of the solution of the corresponding Lyapunov equation $A X+ X A^T =-GG^T$, where $A$ is the matrix obtained from linearizing the second-order differential equation and $G$ depends on the critical part of the eigenfrequencies to be damped. The main result is the efficient approximation and corresponding error bound for the trace of the solution of the Lyapunov equation obtained by dimension reduction, which includes the influence of the right-hand side $G G^T$ and allows us to control the accuracy of the trace approximation. This trace approximation yields a much accelerated optimization algorithm for determining the optimal damping.
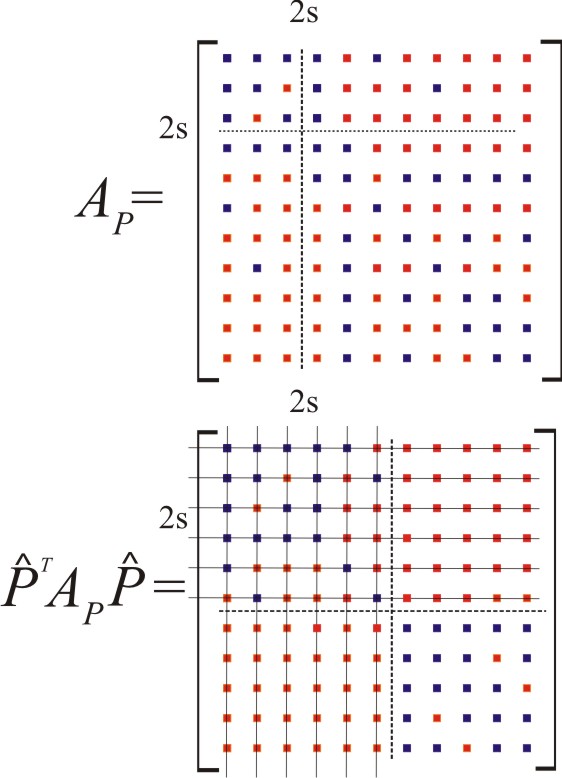
- Peter Benner, Zoran Tomljanović, Ninoslav Truhar
- Dimension reduction for damping optimization in linear vibrating system
- Journal of Applied Mathematics and Mechanics (ZAMM), 91 (3), (2011); 179-191; DOI: 10.1002/zamm.201000077.
Editor's choice of this ZAMM issue!
Preliminary version appeared as Preprint 2/2010, Department of Mathematics, J. J. Strossmayer University of Osijek. (*.PDF) -
ABSTRACT: We consider a mathematical model of a linear vibrational system described by the second-order differential equation $M \ddot{;x}; + D \dot{;x}; + Kx = 0$, where $M$ and $K$ are positive definite matrices, called mass and stiffness, espectively. We consider the case where the damping matrix $D$ is positive semidefinite. The main problem considered in the paper is the construction of efficient algorithm for calculating an optimal damping. As optimization criterion we use the minimization of the average total energy of the system which is equivalent to the minimization of the trace of the solution of the corresponding Lyapunov equation $A X+ X A^T =-I$, where $A$ is the matrix obtained from linearizing the second-order differential equation. Finding the optimal $D$ such that the trace of $X$ is minimal is a very demanding problem, caused by the large number of trace calculations, which are required for bigger matrix dimensions. We propose a dimension reduction to accelerate the optimization process. We will present an approximation of the solution of the structured Lyapunov equation and a corresponding error bound for the approximation. Our algorithm for efficient approximation of the optimal damping is based on this approximation.
- Zoran Tomljanović, Ninoslav Truhar, Krešimir Veselić
- Optimizing a damped system - a case study
- International journal of computer mathematics, 88 (7), (2011); 1533 - 1545
Preliminary version appeared as Preprint 6/2008, Department of Mathematics, J. J. Strossmayer University of Osijek. (*.PDF) -
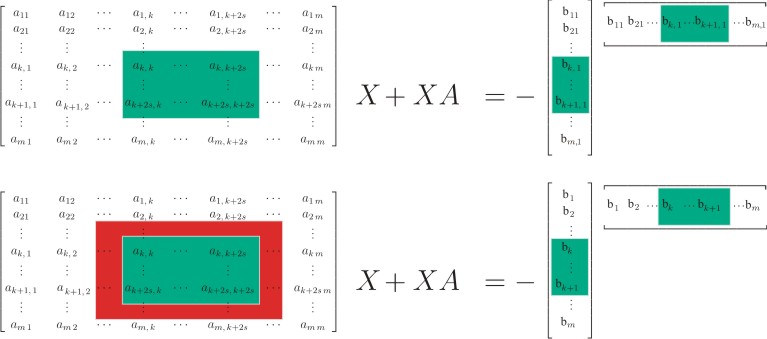
ABSTRACT: We consider a second order damped-vibrational system described by the equation $ M \ddot{;x}; + C(v) \dot{;x}; + K x = 0 $, where $M, C(v), K$ are real, symmetric matrices of order $n$. We assume that the undamped eigenfrequencies (eigenvalues of $(\lambda^2 M + K) x = 0$) $\omega_1, \omega_2, \ldots, \omega_n \, $, are multiple in the sense that $\omega_1 = \omega_2$, $\omega_3 = \omega_4$, \ldots, $\omega_{;n-1}; = \omega_n$, or are given in close pairs $\omega_1 \approx \omega_2$, $\omega_3 \approx \omega_4$, \ldots, $\omega_{;n-1}; \approx \omega_n$. We present a formula which gives the solution of the corresponding phase space Lyapunov equation, which then allows us to calculate the first and second derivatives of the trace of the solution, with no extra cost. This one can serve for the efficient trace minimization.

Preliminary version appeared as Preprint 4/2008, Department of Mathematics, J. J. Strossmayer University of Osijek. (*.PDF)
|
ABSTRACT: The solution to a general Sylvester equation $AX+XB = GF^*$ with a low rank right- hand side is analyzed quantitatively through Low-rank Alternating-Directional- Implicit method (LR-ADI) with exact shifts. New bounds and perturbation bounds on X are obtained. A distinguished feature of these bounds is that they reflect the interplay between the eigenvalue decompositions of A and B and the right-hand side factors G and F. Numerical examples suggest that because of this inclusion of details, new perturbation bounds are much sharper than the existing ones. |
 |
- Ninoslav Truhar , Zoran Tomljanović
- Estimation of optimal damping for mechanical vibrating systems
- International Journal of Applied Mathematics and Mechanics , 5 (2009) , 5; 14-26.
Preliminary version appeared as Preprint 2/2008, Department of Mathematics, J. J. Strossmayer University of Osijek. ( *.PDF) -
ABSTRACT:This paper is concerned with the efficient algorithm for dampers' and viscosity optimization in mechanical systems. Our algorithm optimize simultaneously the dampers' positions and their viscosities. For the criterion for optimization we use minimization of the average total energy of the system which can be done by the minimization of the trace of the solution of the corresponding Lyapunov equation. Efficiency of the algorithm is obtained by new heuristics for finding the optimal dampers' positions and for the approximation of the trace of the solution of the Lyapunov equation.

Papers published at proceedings of international conferences:
- Peter Benner, Zoran Tomljanović, Ninoslav Truhar
- Damping Optimization for Linear Vibrating Systems Using Dimension Reduction (*.PDF)
- In J. Náprstek, J. Horáček, M. Okrouhlík, B. Marvalová, F. Verhulst, and J.T. Sawicki (Eds.),
- Vibration Problems ICOVP 2011. The 10th International Conference on Vibration Problems,, Springer Proceedings in Physics, Vol. 139, Springer-Verlag, pp. 297-305, 2011. [ISBN: 978-94-007-2068-8]
-
ABSTRACT: We consider a mathematical model of a linear vibrational system de- scribed by the second-order system of differential equations $M \ddot{x} + D \dot{x} + Kx = 0$, where M, K and D are positive definite matrices, called mass, stiffness and damp- ing, respectively. We are interested in finding an optimal damping matrix which will damp a certain part of the undamped eigenfrequencies. For this we use a minimiza- tion criterion which minimizes the average total energy of the system. This is equiv- alent to the minimization of the trace of the solution of a corresponding Lyapunov equation. In this paper we consider an algorithm for the efficient optimization of the damping positions based on dimension reduction techniques. Numerical results illustrate the efficiency of our approach.
Profesional papers
- Zoran Tomljanović
- Horner's algorithm and applications
- Osječki matematički list , Vol. 7, No. 2 (2008) 99-106
-
ABSTRACT: In this paper we study Horner's algorithm which is efficient for calculating value of a polynom at a given point. Horner's algorithm we can easily expand to the algorithm with which we can obtain Taylor's expansion around given point. Also, this paper includes illustrative examples and applications of this algorithm.


