Publications

Journal Publications

Khaled Elbassioni, Erik Krohn, Domagoj Matijević, Julian Mestre, Domagoj Ševerdija

Improved Approximations for Guarding 1.5-Dimensional Terrains

Algorithmica, 2011, Volume 60, Number 2, Pages 451-463

(extended abstract appeared in STACS 2009)

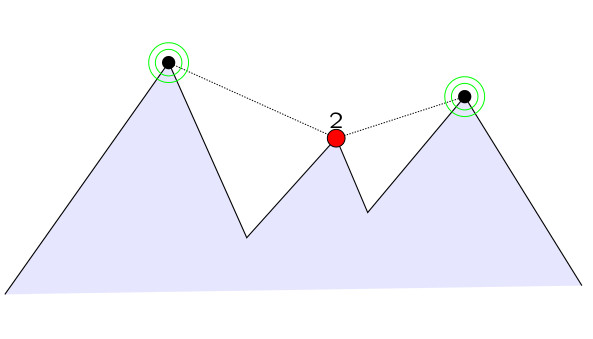
We present a 4-approximation algorithm for the problem of placing the fewest guards on a 1.5D terrain so that every point of the terrain is seen by at least one guard. This improves on the currently best approximation factor of 5. Unlike most of the previous techniques, our method is based on rounding the linear programming relaxation of the corresponding covering problem. Besides the simplicity of the analysis, which mainly relies on decomposing the constraint matrix of the LP into totally balanced matrices, our algorithm, unlike previous work, generalizes to the weighted and partial versions of the basic problem.

F. Belić, Ž. Hocesnki, D. Ševerdija

Naïve matrix multiplication versus Strassen algorithm in multi-thread environment

Tehnički vjesnik, Vol.18 No.3, 2009.

In last few decades computational power of computers has greatly increased. Highest speeds and power are still reserved for super-computers, but high-speed computers have been available for home and amateur users for some time. Normal user most of the time uses only a small amount of computational resources available; even in cases of high-strain, a good part of these resources stays unused. This is partly a result of poor programming. Most of programmers still use single-threaded programming although platforms for parallel programming have been widely available for long time. This article describes using one such platform (.NET Framework) to decrease time needed for multiplication of matrices. This article tries to present what results can be achieved using common equipment and easily acquirable software.

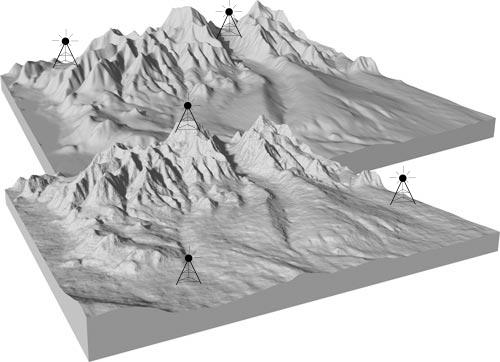
Khaled Elbassioni, Domagoj Matijević, Domagoj Ševerdija

Guarding 1.5D Terrains with Demands

 International Journal of Computer Mathematics , 2012

(extended abstract appeared in EuroCG 2010)

In this paper, we consider the 1.5D terrain guarding problem in which every point on the terrain that is to be covered has an integer demand associated with it. The goal is to find a minimum cardinality set of guards such that each point is guarded by a number of guards satisfying its demand. We present a first constant-factor approximation algorithm for the problem, that is, a  $(1+1/d_\min)$-approximation algorithm, where $d_\min$ is a minimum demand. The algorithm is based on solving appropriate subproblems established by a decomposition of the main problem due to linear programming relaxation of the corresponding covering problem.

Refereed Proceedings

• Guarding 1.5D Terrains with Demands
  K. Elbassioni, D. Matijevic, D. Severdija
  26th European Workshop on Computational Geometry (EuroCG'10 ), pp. 133-136, Dortmund, 2010
• Improved approximations for guarding 1.5-dimensional terrains
  K. Elbassioni, D. Matijevic, J. Mestre, and D. Severdija
  CoRR, abs/0809.0159v1, 2008. and STACS 2009.

Other Publications

I. Matić, D. Ševerdija, S. Škorvaga

Numerička ograničenja kineskog abakusa

to appear in Osječki matematički list, 2009.

We present some aspects of numerical constraints using chinese abacus in standard arithmetic operations with natural numbers.

I. Matić, D. Ševerdija

Grčko-kineski stil u teoriji brojeva

Osječki matematički list. 10 (2010), 1; 43-58

We show how to implement an application of Euclid algorithm on chinese abacus and also consider numerical constraints in applying procedure.

I. Matić, D. Ševerdija

Metodički aspekt kineskog abakusa [ pdf, prezentacija]

Matematika i škola. 11 (2009); 57-62

We present some didactical aspects of using chinese abacus in curriculum for elementary schools. We give some taughts on psychological and social aspects of abacii in everyday appliance.

I. Matić, D. Ševerdija

Metodički aspekt kineskog abakusa II

Matematika i škola. 53 (2010); 106-111

We present some didactical aspects of using chinese abacus in curriculum for elementary schools. We give some taughts on psychological and social aspects of abacii in everyday appliance.

D. Matijević, D. Ševerdija

Problem vidljivosti

Osječki matematički list, 2010.

Za dvije točke kažemo da vide jedna drugu ukoliko ne postoji prepreka koja bi presjecala segment koji ih spaja. Na temelju geometrijskog modela predstaviti ćemo klasične probleme vidljivosti kao što su problem galerije, problem utvrde i problem čuvanja terena. Iznosimo osnovne rezultate vezane uz spomenute probleme i neke od varijacija tih problema.