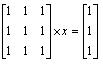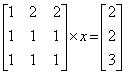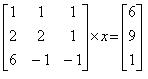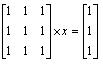Standardni problem predstavlja utvrđivanje postoji li skup vrijednosti za nepoznate,
koji zadovoljava sve jednadžbe istovremeno, kao i pronalaženje takvog skupa ako postoji.
Postojanje skupa rješenja ovisi od jednadžbi, ali i od dostupnih vrijednosti
(radi li se o cijelim brojevima, realnim brojevima, i slično).
Sustavi linearnih jednadžbi spadaju među najstarije matematičke probleme,
i imaju mnoge primjene, kao što su obrada digitalnih signala, procjene, predviđanja,
kao i linearno programiranje ili aproksimacija nelinearnih problema u numeričkoj analizi.
Postoji mnogo načina da se riješi sustav linearnih jednadžbi, koji je zadan s

gdje su x1, x2..., xn nepoznanice, a brojevi a11,a12,..., a mn su koeficijenti sustava. Među najučinkovitijima je Gaussov postupak.
Stavljamo koeficijente u matricu na sljedeći način:

Ako predstavimo svaku matricu slovom, ovo postaje:
Ax=b
gdje je A a m×n matrica, x je vektor stupac sa n članova, a b je vektor stupac sa m članova.
Gaus-Jordanova eliminacija se primjenjuje na sve ove sustave, čak i ako su koeficijenti iz nekog proizvoljnog polja.
Ako je polje beskonačno (kao u slučaju realnih ili kompleksnih brojeva), moguća su samo sljedeća tri slučaja
(točno će jedan biti točan) za svaki dani sustav linearnih jednadžbi:
- sustav nema rješenja
- sustav ima točno jedno rješenje
- sustav ima beskonačno mnogo rješenja.
Vidi primjer!
1) Sustav nema rješenja ako zadana matrica ima linearno zavisne retke ili stupce. Takav sustav zove se još i
nemoguć ili proturječan.



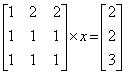
2) Sustav ima točno jedno rješenje ako na jedinstven način možemo zadovoljiti sve tri jednadžbe.

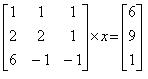
3) Sustav ima beskonačno mnogo rješenja ako više rješenja zadovoljava naš sustav. Takav sustav zove se neodređen.